Fraktal Nedir ve Fraktal Örnekleri
Matematik özellikle geometri 20 yüzyıla gelene kadar Öklid geometrisinde tanımlanan kavramları kullandı; doğrular, düzlemler, üçgenler… Ama gerçek hayatta bulutlar küresel, dağlar konik, göller de eliptik değil. Doğayı daha iyi anlamak ve modellemek için yeni bir geometriye gereksinim vardı. İşte bu da fraktal geometriydi.

Bir şeklin orantılı olarak küçültülmüş veya büyütülmüş modelleriyle inşa edilen örüntülere fraktal adı verilir. Halı veya kilim desenlerini, pisagor ağacını fraktallara örnek verebiliriz. Bir cismi oluşturan parçalar ya da bileşenlerin cismin tamamına benzemesi matematikte “fraktal” olarak adlandırılır. Düzensiz ayrıntılar ya da desenler giderek küçülen ölçeklerde tekrarlanır. Öyle ki bütünün her bir parçası büyütüldüğünde yine cismin bütününe benzer. Fraktal terimi parçalanmış ya da kırılmış anlamına gelen Latince “fractus” sözcüğünden türetilmiştir.
İÇİNDEKİLER
- Fraktal Nedir
- Fraktal Boyut
- Fraktal İlk Hangi Tarihte Ve Kim Tarafından Bulundu
- Teorinin Gelişimi
- Fraktal Nerelerde Kullanılır
- Fraktal Nasıl Oluşturulur
- Fraktallar ve Örüntüler Arasındaki Fark ve İlişkiler
- Fraktal Örnekleri
- Fraktal Soruları Nasıl Çözülür
- Fraktal Görselleri
FRAKTAL NEDİR?
Fraktal; matematikte, çoğunlukla kendine benzeme veya oransal kırılma özelliği gösteren karmaşık geometrik şekillerin ortak adıdır. Fraktallar, klasik, yani Öklid (Euklides) geometrideki kare, daire, küre gibi basit şekillerden çok farklıdır. Bunlar doğadaki, Öklid'çi geometri aracılığıyla tanımlanamayacak pek çok uzamsal açıdan düzensiz olguyu ve düzensiz biçimi tanımlama yeteneğine sahiptir. Fraktal terimi parçalanmış ya da kırılmış anlamına gelen Latince "fractus" sözcüğünden türetilmiştir. İlk olarak 1975'te Polonya asıllı matematikçi Benoit B. Mandelbrot tarafından ortaya atılan kavram, yalnızca matematik değil fiziksel kimya, fizyoloji ve akışkanlar mekaniği gibi değişik alanlar üzerinde önemli etkiler yaratan yeni bir geometri sisteminin doğmasına yol açmıştır.
Yukarıda: Sierpinski üçgeni; mutlak surette simetrik bir fraktal.
Tüm fraktallar kendine benzer ya da en azından tümüyle kendine benzer olmamakla birlikte, çoğu bu özelliği taşır. Kendine benzer bir cisimde cismi oluşturan parçalar ya da bileşenler cismin bütününe benzer. Düzensiz ayrıntılar ya da desenler giderek küçülen ölçeklerde yinelenir ve tümüyle soyut nesnelerde sonsuza değin sürebilir; öyle ki,her parçanın her bir parçası büyütüldüğünde, gene cismin bütününe benzer. Bu fraktal olgusu, kar tanesi ve ağaç kabuğunda kolayca gözlenebilir. Bu tip tüm doğal fraktallar ile matematiksel olarak kendine benzer olan bazıları, stokastik (olasılıksal) yani rastgeledir; bu nedenle ancak istatistiksel olarak ölçeklenirler. Fraktal cisimler, düzensiz biçimli olduklarından ötürü Öklid'çi şekilleri ötelemezler. (Öteleme bakışına sahip bir cisim kendi çevresinde döndürüldüğünde görünümü aynı kalır.)
FRAKTAL BOYUT
Fraktalların belirleyici bir özelliği, fraktal boyut olarak adlandırılan matematiksel bir parametrelerinin olmasıdır. Bu parametrenin bütünüyle geçerli ve basit bir tanımı yoktur. Mandelbrot bu parametreyi Haussdorf boyutu ile denk tutmaktadır. Fraktal boyut, Öklid'çi şekillerin topolojik boyutlarına eşit, fraktallar için topolojik boyutlarından büyüktür. Örneğin Cantor kümesinin fraktal boyutu D=log2/log3 0.6309>0, topolojik boyutu ise DT=0'dır.:14-15
Yukarıda: Bir fraktalı giderek yakınlaşarak izleyen bir animasyon. Simetriye dikkat ediniz.
Kendisinin tam bir kopyasını daha küçük boyutlarda içeren fraktallar için fraktal boyutu ve kendine benzerlik boyutu değerleri aynıdır. Bir şekil kendisine benzeyen (n) kadar kopyadan oluşuyor ve her bir kopya özgün şekle göre, uzunluk olarak, (1/m) büyüklüğünde ise, bu şeklin kendine benzeme boyutu (log n/log m) ile verilir. Yukarıda örnek olarak verilen Sierpinski üçgeni, kendine benzeyen n=3 kopyadan oluşmuş, her bir kopya da özgün şeklin yarısı (m=2) uzunluğundadır; dolayısıyla Sierpinski üçgenin fraktal boyutu (D=log3/log2 1.585)'tir.
FRAKTAL İLK HANGİ TARİHTE VE KİM TARAFINDAN BULUNDU?
İlk olarak 1975’te Polonya asıllı matematikçi Beneoit B. Mandelbrot tarafından ortaya atılan fraktal kavramı, yalnızca matematik değil fizikokimya, fizyoloji ve akışkanlar mekaniği gibi değişik alanlar üzerinde önemli etki-ler meydana getiren yeni bir geometri sisteminin doğmasına yol açmıştır.

TEORİNİN GELİŞİMİ
Benoit Mandelbrot, IBM laboratuvarlarında çalışmaya başladığında Oyun kuramı, iktisat ve emtia fiyatları gibi çeşitli alanlarda çalışan bir mühendisti. Bu çalışmalarını tamamladığında veri iletim hatlarındaki gürültü üzerinde çalışmaya başladı. Mühendisler, veri aktarımı sırasında oluşan gürültü karşısında çaresiz kalmışlardı. Mühendislerin bu soruna bulabildikleri en iyi çare, sinyal gücünü arttırmaktan ileri gidememişti; ama sinyal gücünün arttırılması da tam bir çözüm sağlamamıştır. İletim hatlarındaki gürültü doğası gereği gelişigüzel olmasına rağmen kümeler halinde gelmekteydi. İletişim süresi boyunca hatasız periyotlar arasında hatalı periyotlar yer almaktaydı. Hatalı periyotların incelenmesi, hata paterninin sanıldığından daha karmaşık olduğunu ortaya koymuştur. Mandelbrot, bir günlük veri trafiğini birer saatlik periyotlara ayırdı. Daha sonra, hatanın gözlendiği periyotları ele alıp bu periyotlar yirmişer dakikalık parçalara böldü ve yine gördü ki, bu birer saatlik periyotların içinde de yine hatasız bölümler bulunmaktaydı. Mandelbrot, hatalı bölümler daha kısa zaman aralıklarına bölmeye devam etti. Ve sonunda hatasız periyotların halen var olduğunu gösterdi. Bu arada aykırı bir durum Mandelbrot'un dikkatini çekti: hatalı periyotların hatasız periyotlara oranı periyodun uzunluğundan bağımsız olarak neredeyse sabit kalıyordu.
FRAKTAL NERELERDE KULLANILIR?
Kendine benzerlik ve tamsayı olmayan boyutlu kavramlarıyla birlikte fraktal geometri, istatistiksel mekanikte, özellikle görünürde rastgele özelliklerden oluşan fiziksel sistemlerin incelenmesinde giderek daha yaygın olarak kullanılmaya başlanmıştır. Örneğin, gökada kümelerinin evrendeki dağılımının saptanmasında ve akışkan burgaçlanmalarına ilişkin problemlerin çözülmesinde fraktal benzetimlerden (simülasyon) yararlanılmaktadır. Fraktal geometri bilgisayar grafiklerinde de yararlı olmaktadır. Fraktal algoritma ise, engebeli dağlık araziler ya da ağaçların karışık dal sistemleri gibi karmaşık, çok düzensiz doğal cisimlerin gerçektekine benzer görüntülerinin oluşturulabilmesini olanaklı kılmıştır.
FRAKTAL NASIL OLUŞTURULUR?
Bir şeklin orantılı olarak küçültülmüş ya da büyütülmüşleri ile inşa edilen örüntüler fraktal olarak adlandırılır. Fraktalın bir özelliği de, küçük bir parçasındaki örüntünün şeklin tamamındaki örüntüyle aynı olmasıdır.
Fraktallar ve Örüntüler Arasındaki Fark
Fraktal ve örüntü arasındaki ilişki şöyledir:
Her fraktal bir örüntüdür ancak her örüntü bir fraktal değildir.
Bir örüntünün fraktal olabilmesi için:
- Öncelikle örüntü olabilmesi için bir kurala göre ilerlemesi gerekir.
- Örüntünün büyümesi veya küçülmesi gerekir.
- Bir önceki şekli içinde barındırması gerekir.
FRAKTAL ÖRNEKLERİ
Şimdi hangi örüntülerin niçin fraktal olduğunu veya neden fraktal olmadığını örnek resimlerle inceleyelim.
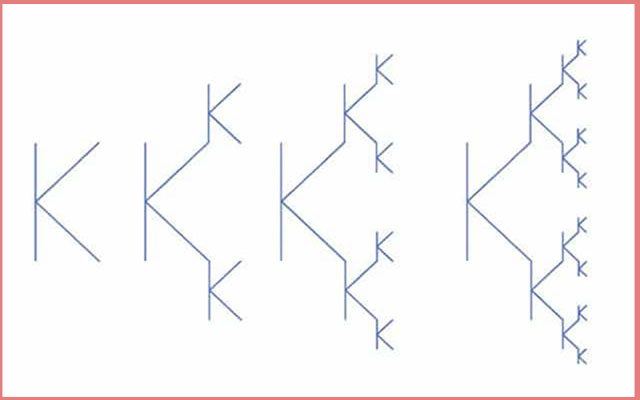
ÖRNEK 1: Aşağıdaki şekilde K harfi %50 küçültülerek şekle eklenmiş ve bir fraktal oluşturulmuştur. Dikkat edilirse her adım bir önceki adımı içinde barındırmaktadır.
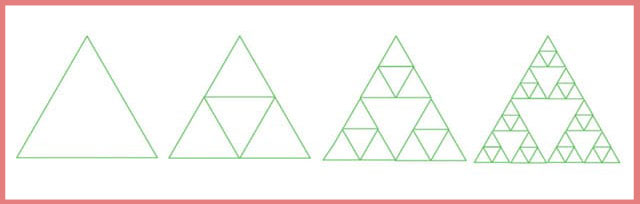
ÖRNEK 2 : Aşağıdaki örüntüde eşkenar üçgen küçültülerek yeni adımlar oluşturulmuştur. Bu örüntü de bir fraktaldır.
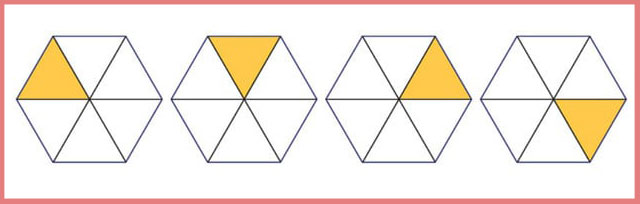
ÖRNEK 3 : Aşağıdaki şekiller belirli bir kurala göre dizildikleri için örüntüdür ancak fraktal olabilmesi için aynı şeklin büyültülmüşü veya küçültülmüşü kullanılması gerekir. Bu yüzden bu örüntü fraktal değildir.
ÖRNEK 4 : Aşağıdaki şekiller belirli bir kurala göre dizildikleri için örüntüdür ancak fraktal olabilmesi için aynı şeklin büyültülmüşü veya küçültülmüşü kullanılması gerekir. Bu yüzden bu örüntü fraktal değildir.
FRAKTAL SORULARI NASIL ÇÖZÜLÜR?
Fraktal soruları genelde iki şekilde sorulur:
1. Soru Tipi: Örüntülerin fraktal olup olmadığı sorulur. Bu sorularda dikkat edilmesi gereken şeklin büyütülmüş veya küçültülmüşünün kullanılması ve örüntünün bir adımının bir önceki adımını içeriyor olmasıdır.
2. Soru Tipi: Fraktalın herhangi bir adımında kullanılan şekil sayısı sorulur. Bu tip sorularda ise kullanılan şekilleri tek tek saymaktan ziyade bir önceki şekile göre ne kadar arttığını bulmak kolaylık sağlar. Bu şekilde bir sayı örüntüsü yakalanabilir. Örnek verecek olursak yukarıdaki K harfi fraktal sorusuna bakalım.
1. Adım: 1
2. Adım: 1+2
3. Adım: 1+2+4
3. Adım: 1+2+4+8
Buradan her adımda 2’nin kuvvetleri şeklinde arttığını görürüz.
En Çok Sevdiğiniz Renk Hangisi?
| İmsak | 04:01 | ||
| Güneş | 05:48 | ||
| Öğle | 13:16 | ||
| İkindi | 17:11 | ||
| Akşam | 20:33 | ||
| Yatsı | 22:12 |
| Takımlar | O | P |
|---|---|---|
| 1. Galatasaray | 38 | 102 |
| 2. Fenerbahçe | 38 | 99 |
| 3. Trabzonspor | 38 | 67 |
| 4. Başakşehir | 38 | 61 |
| 5. Kasımpasa | 38 | 56 |
| 6. Beşiktaş | 38 | 56 |
| 7. Sivasspor | 38 | 54 |
| 8. Alanyaspor | 38 | 52 |
| 9. Rizespor | 38 | 50 |
| 10. Antalyaspor | 38 | 49 |
| 11. Gaziantep FK | 38 | 44 |
| 12. A.Demirspor | 38 | 44 |
| 13. Samsunspor | 38 | 43 |
| 14. Kayserispor | 38 | 42 |
| 15. Hatayspor | 38 | 41 |
| 16. Konyaspor | 38 | 41 |
| 17. Ankaragücü | 38 | 40 |
| 18. Karagümrük | 38 | 40 |
| 19. Pendikspor | 38 | 37 |
| 20. İstanbulspor | 38 | 16 |
| Takımlar | O | P |
|---|---|---|
| 1. Eyüpspor | 34 | 75 |
| 2. Göztepe | 34 | 70 |
| 3. Sakaryaspor | 34 | 60 |
| 4. Bodrumspor | 34 | 57 |
| 5. Ahlatçı Çorum FK | 34 | 56 |
| 6. Kocaelispor | 34 | 55 |
| 7. Boluspor | 34 | 53 |
| 8. Gençlerbirliği | 34 | 51 |
| 9. Bandırmaspor | 34 | 50 |
| 10. Erzurumspor | 34 | 44 |
| 11. Ümraniye | 34 | 43 |
| 12. Manisa FK | 34 | 40 |
| 13. Keçiörengücü | 34 | 40 |
| 14. Adanaspor | 34 | 39 |
| 15. Şanlıurfaspor | 34 | 38 |
| 16. Tuzlaspor | 34 | 38 |
| 17. Altay | 34 | 10 |
| 18. Giresunspor | 34 | 7 |
| Takımlar | O | P |
|---|---|---|
| 1. M.City | 38 | 91 |
| 2. Arsenal | 38 | 89 |
| 3. Liverpool | 38 | 82 |
| 4. Aston Villa | 38 | 68 |
| 5. Tottenham | 38 | 66 |
| 6. Chelsea | 38 | 63 |
| 7. Newcastle | 38 | 60 |
| 8. M. United | 38 | 60 |
| 9. West Ham United | 38 | 52 |
| 10. Crystal Palace | 38 | 49 |
| 11. Brighton | 38 | 48 |
| 12. Bournemouth | 38 | 48 |
| 13. Fulham | 38 | 47 |
| 14. Wolves | 38 | 46 |
| 15. Everton | 38 | 40 |
| 16. Brentford | 38 | 39 |
| 17. Nottingham Forest | 38 | 32 |
| 18. Luton Town | 38 | 26 |
| 19. Burnley | 38 | 24 |
| 20. Sheffield United | 38 | 16 |
| Takımlar | O | P |
|---|---|---|
| 1. Real Madrid | 38 | 95 |
| 2. Barcelona | 38 | 85 |
| 3. Girona | 38 | 81 |
| 4. Atletico Madrid | 38 | 76 |
| 5. Athletic Bilbao | 38 | 68 |
| 6. Real Sociedad | 38 | 60 |
| 7. Real Betis | 38 | 57 |
| 8. Villarreal | 38 | 53 |
| 9. Valencia | 38 | 49 |
| 10. Deportivo Alaves | 38 | 46 |
| 11. Osasuna | 38 | 45 |
| 12. Getafe | 38 | 43 |
| 13. Celta Vigo | 38 | 41 |
| 14. Sevilla | 38 | 41 |
| 15. Mallorca | 38 | 40 |
| 16. Las Palmas | 38 | 40 |
| 17. Rayo Vallecano | 38 | 38 |
| 18. Cadiz | 38 | 33 |
| 19. Almeria | 38 | 21 |
| 20. Granada | 38 | 21 |